Номер 181, страница 52 - гдз по геометрии 7-9 класс учебник Атанасян, Бутузов

181 Постройте окружность данного радиуса, проходящую через две данные точки.

Для решения задачи необходимо найти центр искомой окружности. Пусть даны две точки A и B и радиус R.

Анализ

Центр окружности (обозначим его O) должен быть равноудален от всех точек, лежащих на этой окружности. Поскольку точки A и B должны лежать на искомой окружности, расстояния от центра O до этих точек должны быть равны радиусу R, то есть $OA = OB = R$.

Это означает, что центр O должен удовлетворять двум условиям:

1. Быть равноудаленным от точек A и B. Геометрическое место точек, равноудаленных от концов отрезка, — это серединный перпендикуляр к этому отрезку.
2. Находиться на расстоянии R от точки A (а следовательно, и от точки B). Геометрическое место точек, находящихся на заданном расстоянии от данной точки, — это окружность с центром в данной точке и заданным радиусом.

Таким образом, искомый центр O является точкой пересечения серединного перпендикуляра к отрезку AB и окружности с центром в точке A (или B) и радиусом R.

Построение

1. Соединяем данные точки A и B отрезком прямой.
2. С помощью циркуля и линейки строим серединный перпендикуляр m к отрезку AB.
3. С центром в точке A проводим окружность (или дугу) заданным радиусом R.
4. Находим точки пересечения $O_1$ и $O_2$ серединного перпендикуляра m и построенной окружности. Эти точки и будут центрами искомых окружностей.
5. Если точки пересечения существуют, строим окружность(окружности) с центром(центрами) в $O_1$ (и $O_2$) и радиусом R. Полученные окружности проходят через точки A и B.

Исследование

Количество решений задачи зависит от соотношения между заданным радиусом R и половиной расстояния между точками A и B. Пусть расстояние $|AB| = d$.

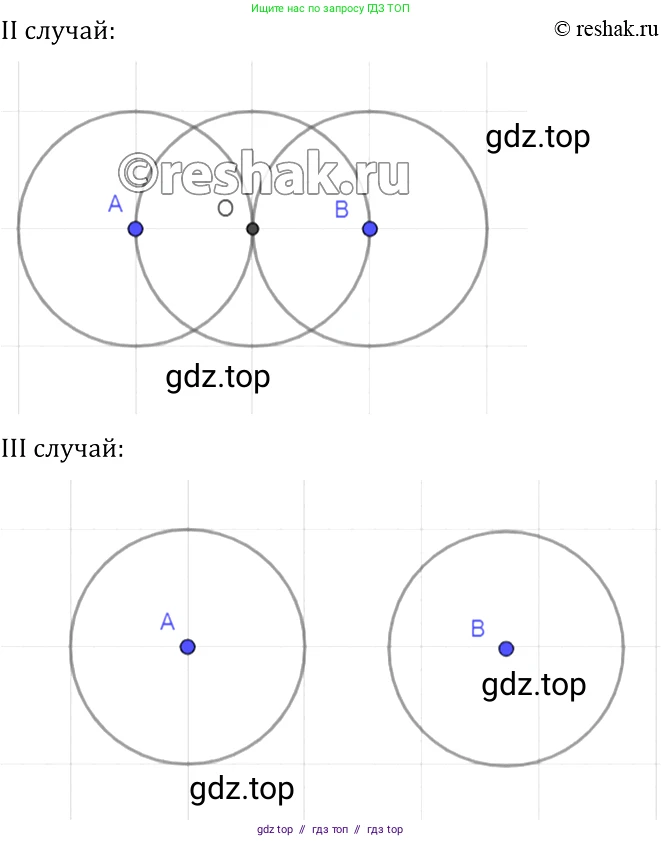
• Если $R > d/2$, окружность, построенная в шаге 3, пересечет серединный перпендикуляр m в двух точках ($O_1$ и $O_2$). Следовательно, задача имеет два решения.
• Если $R = d/2$, окружность коснется серединного перпендикуляра в одной точке — середине отрезка AB. В этом случае задача имеет одно решение (отрезок AB будет диаметром этой окружности).
• Если $R < d/2$, окружность не будет иметь общих точек с серединным перпендикуляром, так как кратчайшее расстояние от точки A до прямой m равно $d/2$. В этом случае задача не имеет решений.

Ответ: Центр искомой окружности находится на пересечении серединного перпендикуляра к отрезку, соединяющему две данные точки, и окружности с центром в одной из этих точек и радиусом, равным данному. Задача может иметь два, одно или ни одного решения в зависимости от соотношения данного радиуса и половины расстояния между точками.